如图,图中的实线是由三段圆弧连接而成的一条封闭曲线 $C$,各段弧所在的圆经过同一点 $P$(点 $P$ 不在 $C$ 上)且半径相等.设第 $i$ 段弧所对的圆心角为 ${\alpha _i}\left(i = 1,2,3\right)$,则 $\cos \dfrac{\alpha _1}{3}\cos \dfrac{{{\alpha _2} + {\alpha _3}}}{3} - \sin \dfrac{\alpha _1}{3}\sin \dfrac{{{\alpha _2} + {\alpha _3}}}{3} = $ .

【难度】
【出处】
2010年高考重庆卷(文)
【标注】
【答案】
$ -\dfrac 1 2 $
【解析】
如图,$\angle APC+\angle CPB+\angle APB=2{\mathrm \pi} $,因为同弧所对的圆心角是圆周角的二倍,所以\[\alpha_1+\alpha_2+\alpha_3=2\cdot 2{\mathrm \pi} =4{\mathrm \pi} ,\]所以\[ \begin{split}&\cos \dfrac{\alpha _1}{3}\cos \dfrac{{{\alpha _2} + {\alpha _3}}}{3} - \sin \dfrac{\alpha _1}{3}\sin \dfrac{{{\alpha _2} + {\alpha _3}}}{3} \\=& \cos \dfrac{{{\alpha _1} + {\alpha _2} + {\alpha _3}}}{3}\\=&\cos {\dfrac {4{\mathrm \pi} } 3 }=-\dfrac 1 2 .\end{split} \]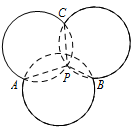

题目
答案
解析
备注