已知以 $F$ 为焦点的抛物线 ${y^2} = 4x$ 上的两点 $ A、B $ 满足 $\overrightarrow {AF} = 3\overrightarrow {FB} $，则弦 $AB$ 的中点到准线的距离为 ．
【难度】
【出处】
2010年高考重庆卷（理）
【标注】
【答案】
$ \dfrac 8 3 $
【解析】
如图，设 $BF = m$，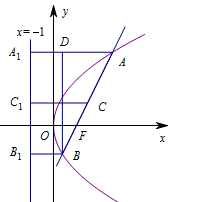
由抛物线的定义，知 $A{A_1} =|AF| =3m$，$B{B_1} =|BF|= m$，
从而 $\triangle ABD$ 中，$ |AD|=2m,|AB|=4m$，$\angle AFx=60^\circ $，
于是直线 $AB$ 的方程为 $y = \sqrt 3 \left(x - 1\right)$，与抛物线方程联立消去 $y$，得 $3{x^2} - 10x + 3 = 0$．
所以 $AB$ 中点 $C $ 到准线距离 $ |CC_1|=\dfrac{{{x_1} + {x_2}}}{2} + 1 = \dfrac{5}{3} + 1 = \dfrac{8}{3}$．
由抛物线的定义，知 $A{A_1} =|AF| =3m$，$B{B_1} =|BF|= m$，从而 $\triangle ABD$ 中，$ |AD|=2m,|AB|=4m$，$\angle AFx=60^\circ $，
于是直线 $AB$ 的方程为 $y = \sqrt 3 \left(x - 1\right)$，与抛物线方程联立消去 $y$，得 $3{x^2} - 10x + 3 = 0$．
所以 $AB$ 中点 $C $ 到准线距离 $ |CC_1|=\dfrac{{{x_1} + {x_2}}}{2} + 1 = \dfrac{5}{3} + 1 = \dfrac{8}{3}$．
题目
答案
解析
备注
