已知函数 $f(x)=x|x-4|$（$x\in\mathbb R$），若存在正实数 $k$，使方程 $f(x)=k$ 在区间 $(2,+\infty)$ 上有两个实数解 $a,b$，其中 $a<b$，则 $ab-2(a+b)$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(-4,0)$
【解析】
函数 $f(x)$ 的图象如下：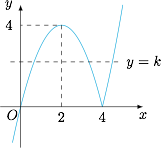
根据题意，有\[2<a<4<b,\]于是\[a(4-a)=b(b-4)=k,\]且 $k$ 的取值范围是 $(0,4)$．注意到所求代数式\[p=ab-2(a+b)=(a-2)(b-2)-4,\]设 $a-2=m$，$b-2=n$，则条件即\[(2+m)(2-m)=(n+2)(n-2)=k,\]也即\[m^2=4-k,n^2=4+k,\]于是\[p=mn-4=\sqrt{16-k^2}-4,\]其取值范围是 $(-4,0)$．
根据题意，有\[2<a<4<b,\]于是\[a(4-a)=b(b-4)=k,\]且 $k$ 的取值范围是 $(0,4)$．注意到所求代数式\[p=ab-2(a+b)=(a-2)(b-2)-4,\]设 $a-2=m$，$b-2=n$，则条件即\[(2+m)(2-m)=(n+2)(n-2)=k,\]也即\[m^2=4-k,n^2=4+k,\]于是\[p=mn-4=\sqrt{16-k^2}-4,\]其取值范围是 $(-4,0)$．
题目
答案
解析
备注
