已知函数 $f(x)=x^3-6x^2+12x$，$a_1,a_2,\cdots,a_{10}$ 均为非负实数，且 $\displaystyle \sum_{i=1}^{10}a_i=18$，则 $M=\displaystyle \sum_{i=1}^{10}f(a_i)$ 的最小值是 ，使 $M$ 取最小值的有序数组 $(a_1,a_2,\cdots,a_{10})$ 的个数为 ．
【难度】
【出处】
无
【标注】
【答案】
$54$，$210$
【解析】
如图，作函数 $f(x)$ 过原点的切线．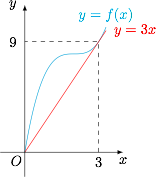
于是有\[\forall x\in [0,+\infty),f(x)\geqslant 3x,\]等号当且仅当 $x=0,3$ 时取得．因此\[ \sum_{i=1}^{10}f(a_i)\geqslant 3\cdot \sum_{i=1}^{10}a_i=54,\]等号当且仅当 $a_i$（$i=1,2,\cdots,10$）中有 $6$ 个 $3$ 和 $4$ 个 $0$ 时取得，对应有序数组的个数为 ${\rm C}_{10}^{4}=210$．
于是有\[\forall x\in [0,+\infty),f(x)\geqslant 3x,\]等号当且仅当 $x=0,3$ 时取得．因此\[ \sum_{i=1}^{10}f(a_i)\geqslant 3\cdot \sum_{i=1}^{10}a_i=54,\]等号当且仅当 $a_i$（$i=1,2,\cdots,10$）中有 $6$ 个 $3$ 和 $4$ 个 $0$ 时取得，对应有序数组的个数为 ${\rm C}_{10}^{4}=210$．
题目
答案
解析
备注
