已知数列 $\{a_n\}$ 满足 $a_{n+1}=a_n^2-2$（$n\in\mathbb N^{\ast}$）．若存在常数 $A$，对于任意 $n\in\mathbb N^{\ast}$，恒有 $|a_n|\leqslant A$，则 $a_1$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$[-2,2]$
【解析】
迭代函数为 $f(x)=x^2-2$，对应的不动点为 $x=-1,2$，如图．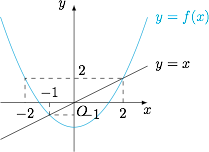
由 $f(x)$ 的性质知，当 $x\in[-2,2]$ 时，$f(x)\in[-2,2]$．所以 $a_1\in[-2,2]$ 时，恒有 $|a_n|\geqslant 2$，取 $A=2$ 即可．
当 $a_1>2$ 时，因为\[\dfrac{a_{n+1}-2}{a_n-2}=a_n+2,\]所以可以由数学归纳法证明数列 $\{a_n\}$ 递增，从而可以递推得到\[a_n-2\geqslant 4^{n-m}\left(a_m-2\right),\]因此数列 $\{a_n\}$ 无界．
当 $a_1<-2$ 时，有 $a_2>2$，结合前面的讨论知，此时数列 $\{a_n\}$ 无界．
综上，$a_1$ 的取值范围是 $[-2,2]$．
由 $f(x)$ 的性质知，当 $x\in[-2,2]$ 时，$f(x)\in[-2,2]$．所以 $a_1\in[-2,2]$ 时，恒有 $|a_n|\geqslant 2$，取 $A=2$ 即可．当 $a_1>2$ 时，因为\[\dfrac{a_{n+1}-2}{a_n-2}=a_n+2,\]所以可以由数学归纳法证明数列 $\{a_n\}$ 递增，从而可以递推得到\[a_n-2\geqslant 4^{n-m}\left(a_m-2\right),\]因此数列 $\{a_n\}$ 无界．
当 $a_1<-2$ 时，有 $a_2>2$，结合前面的讨论知，此时数列 $\{a_n\}$ 无界．
综上，$a_1$ 的取值范围是 $[-2,2]$．
题目
答案
解析
备注
