已知函数 $f(x)=\begin{cases} 1-|x+1|,&x<1,\\ x^2-4x+2,&x\geqslant 1,\end{cases}$ 则函数 $g(x)=2^{|x|}\cdot f(x)-2$ 的零点个数为 ．
【难度】
【出处】
无
【标注】
【答案】
$2$
【解析】
问题即求函数 $f(x)$ 的图象与函数 $h(x)=2^{1-|x|}$ 的图象的公共点个数，如图．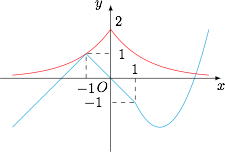
容易确定在区间 $(-1,0)$ 上\[h(x)>1>f(x),\]在区间 $(0,2)$ 上\[h(x)>0>f(x),\]而在区间 $[2,+\infty)$ 上，$h(x)$ 单调递减，$f(x)$ 单调递增，两者图象有唯一公共点．
在区间 $(-\infty,-1]$ 上，有\[h(-1)=f(-1)=-1,\]而当 $x<-1$ 时，有\[h(x)=2^{1+x}> \ln 2\cdot (x+1)+1> x+1+1=f(x),\]因此在区间 $(-\infty,-1)$ 上两者图象没有公共点．
综上所述，所求零点的个数为 $2$．
容易确定在区间 $(-1,0)$ 上\[h(x)>1>f(x),\]在区间 $(0,2)$ 上\[h(x)>0>f(x),\]而在区间 $[2,+\infty)$ 上，$h(x)$ 单调递减，$f(x)$ 单调递增，两者图象有唯一公共点．在区间 $(-\infty,-1]$ 上，有\[h(-1)=f(-1)=-1,\]而当 $x<-1$ 时，有\[h(x)=2^{1+x}> \ln 2\cdot (x+1)+1> x+1+1=f(x),\]因此在区间 $(-\infty,-1)$ 上两者图象没有公共点．
综上所述，所求零点的个数为 $2$．
题目
答案
解析
备注
