记 $m={\bf a}\cdot {\bf e}$，$n={\bf b}\cdot {\bf e}$．${\bf a}$，${\bf b}$，${\bf e}$ 对应的角分别为 $0$，$\arccos\dfrac 14$，$\theta$，如图．由图形的对称性不妨设 $\theta\in\left[-\arcsin\dfrac 14,\pi-\arcsin\dfrac 14\right)$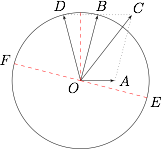．根据题意有\[\begin{split} |OC|&=|{\bf a}+{\bf b}|=\sqrt 6,\\ |OD|&=|{\bf a}-{\bf b}|=2.\end{split}\]情形一 $m\cdot n\geqslant 0$．此时\[|m|+|n|=|m+n|=|({\bf a}+{\bf b})\cdot {\bf e}|,\]此时 $\theta$ 的取值范围是 $\left[-\arcsin\dfrac 14,\dfrac{\pi}2\right]$，于是 $|m|+|n|$ 的取值范围是 $\left[\dfrac {\sqrt{15}}4,\sqrt 6\right]$．
情形二 $m\cdot n< 0$．此时\[|m|+|n|=|m-n|=|({\bf a}-{\bf b})\cdot {\bf e}|,\]此时 $\theta$ 的取值范围是 $\left(\dfrac{\pi}2,\pi-\arcsin\dfrac 14\right)$，于是 $ |m|+|n| $ 的取值范围是 $ \left(\dfrac {\sqrt {15}}4,2\right]$．
综上所述，所求的取值范围是 $\left[\dfrac{\sqrt {15}}4,\sqrt 6\right]$．