一只小船以 $10\mathrm{m}/s$ 的速度由南向北匀速驶过湖面，在离湖面高 $20\mathrm{m}$ 的桥上，一辆汽车由西向东以 $20\mathrm{m}/s$ 的速度前进，如图所示，现在小船在水面 $P$ 点以南的 $40\mathrm{m}$ 处，汽车在桥上 $Q$ 点以西 $30\mathrm{m}$ 处，其中 $PQ\perp$ 水面，则小船与汽车间的最短距离为 $\mathrm{m}$（不考虑汽车与小船本身的尺寸大小）．
【难度】
【出处】
2006年第十七届"希望杯"全国数学邀请赛高二（一试）
【标注】
【答案】
$30$
【解析】
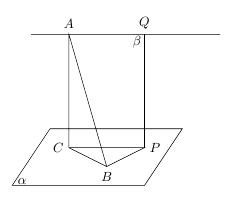设经过时间 $t$ 汽车在 $A$ 点，船在 $B$ 点，如图所示，则有$$\begin{split} & AQ=30-20t,\\&BP=40-10t,\\
&PQ=20,\end{split}$$且$$AQ\perp BP,PQ\perp AQ,PQ\perp PB,$$设小船所在平面为 $\alpha$，由 $AQ,QP$ 确定的平面为 $\beta$，记 $\alpha \cap\beta=l$，由于$$\left(AQ\parallel \alpha\right)\land\left(AQ\subset \beta\right),$$所以 $AQ\parallel l$，又 $AQ\perp PQ$，所以 $PQ\perp l$，又因为$$\left(PQ\perp PB\right)\land\left(l\cap PB=P\right),$$所以 $PQ\perp \alpha$，作 $AC\parallel PQ$，则 $AC\perp \alpha$，连结 $CB$，则 $AC\perp CB$，进而$$\left(AQ\perp BP\right)\land\left(CP\parallel AQ\right),$$因此 $CP\perp BP$，于是$$\begin{split} AB^2&=AC^2+BC^2\\
&=PQ^2+PB^2+PC^2 \\
&=100[5(t-2)^2+9].\end{split}$$故当 $t=2$ 时，最短距离为 $30\mathrm{m}$．
题目
答案
解析
备注
