已知 $f(x)=(x-2)^2\cdot {\rm e}^x+a{\rm e}^{-x}$，$g(x)=2a|x-2|$，若关于 $x$ 的方程 $f(x)=g(x)$ 有 $6$ 个实数解，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(1,\dfrac{{\rm e}^2}{2{\rm e}-1}\right)$
【解析】
方程即\[\left(|x-2|\cdot{\rm e}^x\right)^2-2a\left(|x-2|\cdot{\rm e}^x\right)+a=0,\]令 $t=|x-2|\cdot {\rm e}^x$，利用导数研究其图象，如图．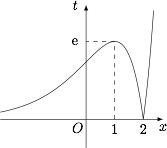
可得 $t$ 的不同取值与 $x$ 的取值个数 $n$ 之间的关系为\[\begin{array} {c|ccccc}\hline
t&(-\infty,0)&0&(0,{\rm e})&{\rm e}&({\rm e},+\infty)\\ \hline
n&0&1&3&2&1\\ \hline
\end{array}\]因此题意即关于 $t$ 的方程\[t^2-2at+a=0\]在 $(0,{\rm e})$ 上有 $2$ 个实数解，也即\[\begin{cases} 0<a<{\rm e},\\ \left(t^2-2at+a\right)\Big|_{t=0}>0,\\ \left(t^2-2at+a\right)\Big|_{t={\rm e}}>0,\\ \Delta=4a^2-4a>0,\end{cases}\]解得\[1<a<\dfrac{{\rm e}^2}{2{\rm e}-1}.\]综上所述，实数 $a$ 的取值范围是 $\left(1,\dfrac{{\rm e}^2}{2{\rm e}-1}\right)$．
可得 $t$ 的不同取值与 $x$ 的取值个数 $n$ 之间的关系为\[\begin{array} {c|ccccc}\hlinet&(-\infty,0)&0&(0,{\rm e})&{\rm e}&({\rm e},+\infty)\\ \hline
n&0&1&3&2&1\\ \hline
\end{array}\]因此题意即关于 $t$ 的方程\[t^2-2at+a=0\]在 $(0,{\rm e})$ 上有 $2$ 个实数解，也即\[\begin{cases} 0<a<{\rm e},\\ \left(t^2-2at+a\right)\Big|_{t=0}>0,\\ \left(t^2-2at+a\right)\Big|_{t={\rm e}}>0,\\ \Delta=4a^2-4a>0,\end{cases}\]解得\[1<a<\dfrac{{\rm e}^2}{2{\rm e}-1}.\]综上所述，实数 $a$ 的取值范围是 $\left(1,\dfrac{{\rm e}^2}{2{\rm e}-1}\right)$．
题目
答案
解析
备注
