过抛物线 $x^2=4y$ 的焦点 $F$ 作直线 $l$ 与抛物线交于 $A$，$B$，记抛物线在 $A$，$B$ 两点处的切线 $l_1$，$l_2$ 的交点为 $P$，则 $\triangle ABP$ 面积的最小值为 ．
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（一测）
【标注】
【答案】
$4$
【解析】
如图．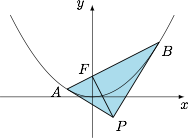
根据题意，有 $P$ 点位于直线 $y=-1$ 上，且 $PF\perp AB$，于是 $\triangle ABP$ 的面积\[S=\dfrac 12\cdot AB\cdot PF\geqslant \dfrac 12\cdot 4\cdot 2=4,\]等号当 $P$ 位于 $(0,-1)$ 时取得，此时 $AB$ 和 $PF$ 同时取得最小值．因此所求面积的最小值为 $4$．
根据题意，有 $P$ 点位于直线 $y=-1$ 上，且 $PF\perp AB$，于是 $\triangle ABP$ 的面积\[S=\dfrac 12\cdot AB\cdot PF\geqslant \dfrac 12\cdot 4\cdot 2=4,\]等号当 $P$ 位于 $(0,-1)$ 时取得，此时 $AB$ 和 $PF$ 同时取得最小值．因此所求面积的最小值为 $4$．
题目
答案
解析
备注
