如图所示，将一块半径为 $1$ 的半圆形钢板截成等腰梯形 $ABCD$ 的形状，它的下底 $AB$ 是半圆直径，上底 $CD$ 的端点在圆周上．这个梯形的周长 $y$ 和腰长 $x$ 之间的函数式为 ；面积 $S$ 和下底角 $\theta$ 之间的函数式为 ．
【难度】
【出处】
2007年第十八届"希望杯"全国数学邀请赛高一（一试）
【标注】
【答案】
$-x^2+2x+4(0<x<\sqrt 2)$；$\sin 2\theta-\dfrac 12\sin4\theta\left(\dfrac {\pi}{4}<\theta<\dfrac {\pi}{2}\right)$
【解析】
如图，设半圆的圆心为 $O$，连接 $OC,OD$．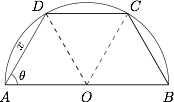
根据题意，有\[\sin\dfrac {\angle AOD}2=\dfrac x2,\]于是梯形 $ABCD$ 的周长\[\begin{split} y&=AB+2AD+CD=2+2x+2\sin\dfrac{\angle DOC}2\\
&=2+2x+2\sin\dfrac{\pi-2\angle AOD}2\\
&=2+2x+2\cos\angle AOD\\
&=2+2x+2\left(1-2\sin^2\dfrac{\angle AOD}2\right)\\
&=-x^2+2x+4,\end{split}\]其中 $0<x<\sqrt 2$．进而\[\begin{split} S&=2\triangle AOD+\triangle COD\\
&=2\cdot \dfrac 12\sin\angle AOD+\dfrac 12\sin\angle DOC\\
&=\sin(\pi-2\theta)+\dfrac 12\sin(4\theta-\pi)\\
&=\sin 2\theta-\dfrac 12\sin4\theta,\end{split}\]其中 $0<\theta<\dfrac{\pi}4$．
根据题意，有\[\sin\dfrac {\angle AOD}2=\dfrac x2,\]于是梯形 $ABCD$ 的周长\[\begin{split} y&=AB+2AD+CD=2+2x+2\sin\dfrac{\angle DOC}2\\&=2+2x+2\sin\dfrac{\pi-2\angle AOD}2\\
&=2+2x+2\cos\angle AOD\\
&=2+2x+2\left(1-2\sin^2\dfrac{\angle AOD}2\right)\\
&=-x^2+2x+4,\end{split}\]其中 $0<x<\sqrt 2$．进而\[\begin{split} S&=2\triangle AOD+\triangle COD\\
&=2\cdot \dfrac 12\sin\angle AOD+\dfrac 12\sin\angle DOC\\
&=\sin(\pi-2\theta)+\dfrac 12\sin(4\theta-\pi)\\
&=\sin 2\theta-\dfrac 12\sin4\theta,\end{split}\]其中 $0<\theta<\dfrac{\pi}4$．
题目
答案
解析
备注
