过抛物线 ${x^2} = 2py\left(p>0\right)$ 的焦点作斜率为 $ 1 $ 的直线与该抛物线交于 $A,B$ 两点，$A,B$ 在 $x$ 轴上的正射影分别为 $D,C$．若梯形 $ABCD$ 的面积为 $12\sqrt 2 $，则 $p = $ ．
【难度】
【出处】
2010年高考湖南卷（理）
【标注】
【答案】
$ 2 $
【解析】
如图，设 $A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，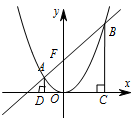
因为直线的斜率是 $1$，所以 $CD=\dfrac {\sqrt2} 2 AB$，所以梯形 $ABCD$ 的面积为 $\dfrac 1 2 \left(AD+BC\right)\cdot DC=\dfrac 1 2 \left(y_1+y_2\right)\cdot \dfrac {\sqrt2} 2 \left(y_1+y_2+p\right)=12\sqrt2 \quad \cdots \cdots ① $．
将 $AB$ 的方程和抛物线方程 $x^2=2py$ 联立消掉 $x$ 得 $y^2-3py+\dfrac {p^2} 4 =0$，
由韦达定理可得 $y_1+y_2=3p \quad \cdots \cdots ② $，
①② 联立可求得 $p=2$．
因为直线的斜率是 $1$，所以 $CD=\dfrac {\sqrt2} 2 AB$，所以梯形 $ABCD$ 的面积为 $\dfrac 1 2 \left(AD+BC\right)\cdot DC=\dfrac 1 2 \left(y_1+y_2\right)\cdot \dfrac {\sqrt2} 2 \left(y_1+y_2+p\right)=12\sqrt2 \quad \cdots \cdots ① $．将 $AB$ 的方程和抛物线方程 $x^2=2py$ 联立消掉 $x$ 得 $y^2-3py+\dfrac {p^2} 4 =0$，
由韦达定理可得 $y_1+y_2=3p \quad \cdots \cdots ② $，
①② 联立可求得 $p=2$．
题目
答案
解析
备注
