查看数据源：5a151b24feda740009b6ea1e
已知集合 $M=\{(x,y)\mid y=3-x,0\leqslant x\leqslant 3\}$，$N=\{(x,y)\mid y=-x^2-mx+1\}$，$M\cap N$ 只有一个元素，则实数 $m$ 的取值范围是 ．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（一试）
【标注】
  • 方法
    >
    代数处理
    >
    分离变量法
  • 知识点
    >
    函数
    >
    集合与映射
    >
    集合的运算
【答案】
$\left(-\infty,-\dfrac 83\right)\cup\left\{1-2\sqrt 2\right\}$
【解析】
若 $M\cap N$ 只有一个元素，则关于 $x$ 的方程$$3-x=-x^2-mx+1$$在 $[0,3]$ 上有一个实数解．显然 $x=0$ 不符合题意，当 $0<x\leqslant 3$ 时，题目转化为$$1-m=x+\dfrac 2x$$在 $(0,3]$ 上有一个实数解．所以$$1-m>\dfrac {11}{3}\lor 1-m=2\sqrt 2,$$故 $m$ 的取值范围是 $\left(-\infty,-\dfrac 83\right)\cup\left\{1-2\sqrt 2\right\}$．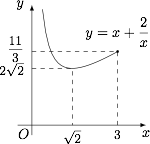
题目 答案 解析 备注
0.137973s