已知非零向量 $\overrightarrow a,\overrightarrow b$ 的夹角为 $60^{\circ}$，且 $\left|\overrightarrow b\right|=2\left|\overrightarrow a\right|$，若 $\overrightarrow a+k\overrightarrow b(k>0)$ 与向量 $\overrightarrow a$ 的夹角为 $30^{\circ}$，则 $k=$ ，此时 $\dfrac{\left|\overrightarrow a\right|}{\left|\overrightarrow a+k\overrightarrow b\right|}=$ ．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$\dfrac 12$；$\dfrac{\sqrt 3}{3}$
【解析】
如图所示，设 $\overrightarrow{OA}=\overrightarrow a$，$\overrightarrow{OD}=\overrightarrow b$，$\overrightarrow {OB}=k\overrightarrow b$．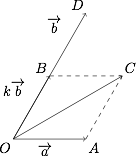
因为 $\overrightarrow a$ 与 $\overrightarrow b$ 的夹角为 $60^{\circ}$，$\overrightarrow a+k\overrightarrow b$ 与 $\overrightarrow a$ 的夹角为 $30^{\circ}$，所以 $k>0$ 且四边形 $OACB$ 为菱形，因此$$|k\overrightarrow b|=|\overrightarrow a|,$$所以$$k=\dfrac 12.$$进而$$\dfrac{|\overrightarrow a|}{|\overrightarrow a+k\overrightarrow b|}=\dfrac{OA}{OC}=\dfrac{\sqrt 3}{3}.$$
因为 $\overrightarrow a$ 与 $\overrightarrow b$ 的夹角为 $60^{\circ}$，$\overrightarrow a+k\overrightarrow b$ 与 $\overrightarrow a$ 的夹角为 $30^{\circ}$，所以 $k>0$ 且四边形 $OACB$ 为菱形，因此$$|k\overrightarrow b|=|\overrightarrow a|,$$所以$$k=\dfrac 12.$$进而$$\dfrac{|\overrightarrow a|}{|\overrightarrow a+k\overrightarrow b|}=\dfrac{OA}{OC}=\dfrac{\sqrt 3}{3}.$$
题目
答案
解析
备注
