若直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有且只有 $1$ 个公共点，则 $b$ 的取值范围是 ，若直线与曲线有 $2$ 个公共点，则 $b$ 的取值范围是 ．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$[-2,2)\cup\left\{2\sqrt 2\right\}$；$\left[2,2\sqrt 2\right)$
【解析】
如图所示，曲线 $y=\sqrt{4-x^2}$ 表示圆 $x^2+y^2=1$ 的上半圆，考虑直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有公共点，临界情况为直线与圆相切或直线过点 $(2,0)$，$(-2,0)$．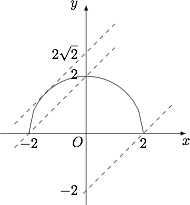
当直线过点 $(2,0)$ 时，$b=-2$；当直线过点 $(-2,0)$ 时，$b=2$；当直线与圆相切时，$b=2\sqrt 2$．因此若直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有一个公共点，则 $b$ 的取值范围是 $[-2,2)\cup\left\{2\sqrt 2\right\}$；若直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有两个公共点，则 $b$ 的取值范围是 $\left[2,2\sqrt 2\right)$．
当直线过点 $(2,0)$ 时，$b=-2$；当直线过点 $(-2,0)$ 时，$b=2$；当直线与圆相切时，$b=2\sqrt 2$．因此若直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有一个公共点，则 $b$ 的取值范围是 $[-2,2)\cup\left\{2\sqrt 2\right\}$；若直线 $y=x+b$ 与曲线 $y=\sqrt{4-x^2}$ 有两个公共点，则 $b$ 的取值范围是 $\left[2,2\sqrt 2\right)$．
题目
答案
解析
备注
