已知长方体 $ABCD-A_1B_1C_1D_1$ 的棱长 $AB=10$，$BC=8$，$AA_1=6$．点 $O$ 在棱长 $AB$ 上，$AO=6$．现以 $O$ 为球心，$r$ 为半径作一球面，则与长方体的 $6$ 个面都有公共点的球面所对应的半径 $r$ 的取值范围为 ；若 $r=11$，则该球面与长方体的 $6$ 个面中的 个面有公共点．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$\left[8,6\sqrt 2\right]$；$3$
【解析】
如图，设点 $O$ 到平面 $AB_1,DC_1,AD_1,BC_1,AC,A_1C_1$ 上的点的距离分别为 $d_1,d_2,d_3,d_4,d_5,d_6$．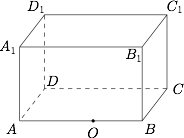
相应的取值范围如下表：$$\begin{array}{|c|c|c|}\hline
d_1&d_2&d_3\\ \hline
\left[0,6\sqrt 2\right]&\left[8,2\sqrt{34}\right]&\left[6,2\sqrt{34}\right]\\ \hline
d_4&d_5&d_6\\ \hline
\left[4,2\sqrt{29}\right]&\left[0,10\right]&\left[6,2\sqrt{34}\right]\\ \hline
\end{array}$$则若以 $O$ 为球心半径为 $r$ 的球面与长方体的 $6$ 个面都有公共点，则 $r$ 的取值范围为 $\left[8,6\sqrt 2\right]$；若 $r=11$，则该球面与长方体的面 $DC_1,AD_1,A_1C_1$ 有公共点．
相应的取值范围如下表：$$\begin{array}{|c|c|c|}\hlined_1&d_2&d_3\\ \hline
\left[0,6\sqrt 2\right]&\left[8,2\sqrt{34}\right]&\left[6,2\sqrt{34}\right]\\ \hline
d_4&d_5&d_6\\ \hline
\left[4,2\sqrt{29}\right]&\left[0,10\right]&\left[6,2\sqrt{34}\right]\\ \hline
\end{array}$$则若以 $O$ 为球心半径为 $r$ 的球面与长方体的 $6$ 个面都有公共点，则 $r$ 的取值范围为 $\left[8,6\sqrt 2\right]$；若 $r=11$，则该球面与长方体的面 $DC_1,AD_1,A_1C_1$ 有公共点．
题目
答案
解析
备注
