在平面内给定正六边形 $A_1A_2A_3A_4A_5A_6$,对于该平面内任意一点 $M$,若适当选取表达式 $\pm\overrightarrow{MA_1}\pm \overrightarrow{MA_2}\pm \overrightarrow{MA_3}\pm \overrightarrow{MA_4}\pm \overrightarrow{MA_5}\pm \overrightarrow{MA_6}$ 中的正负号,则可使该式为零,如 (给出一个向量表达式即可).
【难度】
【出处】
2007年第十八届“希望杯”全国数学邀请赛高一(二试)
【标注】
【答案】
$-\overrightarrow{MA_1}+\overrightarrow{MA_2}+\overrightarrow{MA_3}-\overrightarrow{MA_4}+\overrightarrow{MA_5}-\overrightarrow{MA_6}$
【解析】
如图,有$$\overrightarrow{A_2A_1}+\overrightarrow{A_4A_5}+\overrightarrow{A_6A_3}=\overrightarrow 0,$$将起点都换成 $M$ 可得$$\overrightarrow{MA_2}-\overrightarrow{MA_1}+\overrightarrow{MA_5}-\overrightarrow{MA_4}+\overrightarrow{MA_3}-\overrightarrow{MA_6}=\overrightarrow 0.$$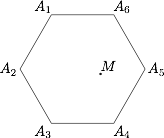

题目
答案
解析
备注