在如图所示的三棱柱中，点 $A$，$BB_1$ 的中点 $M$ 以及 $B_1C_1$ 的中点 $N$ 所决定的平面把三棱柱割成体积不同的两部分，则较小部分的体积和原三棱柱的体积之比为 \((\qquad)\) 
【难度】
【出处】
2014年湖南省高中数学竞赛
【标注】
【答案】
B
【解析】
连结 $NM$ 与 $CB$ 的延长线交于 $D$，连结 $AD$．连结 $MN$ 与 $CC_1$ 的延长线交于 $E$，依题意知点 $E$ 也在 $A$，$M$，$N$，$D$ 所确定的平面内．
设平面 $AMN$ 交 $A_1C_1$ 于 $F$．令原三棱柱底面积为 $S$，高为 $h$．平面将原三棱柱分为上下两个部分体积分别记为 $V_1$，$V_2$．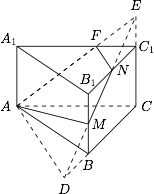
由于 $M$ 是 $BB_1$ 的中点，$\triangle B_1NM \cong \triangle BDM$，故$$\dfrac {DB}{BC}=\dfrac 12,$$从而$$S_{\triangle ADC}=\dfrac 32S.$$同理有$$\dfrac {EC_1}{C_1C}=\dfrac 12.$$又\[\begin{split}V_2&=V_{E-ADC}-V_{E-N{C_1}F}-V_{M-ADB}\\&=\dfrac 13 \times \dfrac 32S \times \dfrac 32h-\dfrac 13\left(\dfrac 32S\times \dfrac 19\right)\times \dfrac 12h -\dfrac 13\times \dfrac S2\times \dfrac h2 \\ &=\dfrac {23}{36}Sh,\end{split}\]于是$$ V_1=Sh-\dfrac {23}{36}Sh=\dfrac {13}{36}Sh.$$故较小部分的体积和原三棱柱的体积之比为 $\dfrac {V_1}{V}=\dfrac {13}{36}$．
设平面 $AMN$ 交 $A_1C_1$ 于 $F$．令原三棱柱底面积为 $S$，高为 $h$．平面将原三棱柱分为上下两个部分体积分别记为 $V_1$，$V_2$．
由于 $M$ 是 $BB_1$ 的中点，$\triangle B_1NM \cong \triangle BDM$，故$$\dfrac {DB}{BC}=\dfrac 12,$$从而$$S_{\triangle ADC}=\dfrac 32S.$$同理有$$\dfrac {EC_1}{C_1C}=\dfrac 12.$$又\[\begin{split}V_2&=V_{E-ADC}-V_{E-N{C_1}F}-V_{M-ADB}\\&=\dfrac 13 \times \dfrac 32S \times \dfrac 32h-\dfrac 13\left(\dfrac 32S\times \dfrac 19\right)\times \dfrac 12h -\dfrac 13\times \dfrac S2\times \dfrac h2 \\ &=\dfrac {23}{36}Sh,\end{split}\]于是$$ V_1=Sh-\dfrac {23}{36}Sh=\dfrac {13}{36}Sh.$$故较小部分的体积和原三棱柱的体积之比为 $\dfrac {V_1}{V}=\dfrac {13}{36}$．
题目
答案
解析
备注
