曲线 $x^2+y^2-5=|2x-2|$ 围成的图形的面积是 ．
【难度】
【出处】
2011年第二十二届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
$8\pi+4$
【解析】
如图．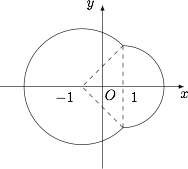
当 $x\geqslant 1$ 时，曲线为$$(x-1)^2+y^2=4.$$所围成的图形面积为$$\dfrac 12 \cdot \pi \cdot 4=2\pi;$$当 $x<1$ 时，曲线为$$(x+1)^2+y^2=8,$$所围成的面积为$$8\pi-\left(2\pi-\dfrac 12 \cdot 2\sqrt 2\cdot 2\sqrt 2\right)=6\pi+4.$$故曲线 $x^2+y^2-5=|2x-2|$ 围成图形的面积为 $8\pi+4$．
当 $x\geqslant 1$ 时，曲线为$$(x-1)^2+y^2=4.$$所围成的图形面积为$$\dfrac 12 \cdot \pi \cdot 4=2\pi;$$当 $x<1$ 时，曲线为$$(x+1)^2+y^2=8,$$所围成的面积为$$8\pi-\left(2\pi-\dfrac 12 \cdot 2\sqrt 2\cdot 2\sqrt 2\right)=6\pi+4.$$故曲线 $x^2+y^2-5=|2x-2|$ 围成图形的面积为 $8\pi+4$．
题目
答案
解析
备注
