在正三棱锥 $P-ABC$ 中，有一半球，其底面与正三棱锥的底面重合，正三棱锥的三个侧面都和半球相切．如果半球的半径等于 $1$，则正三棱锥的体积最小时，正三棱锥的高等于 \((\qquad)\)
【难度】
【出处】
2009年全国高中数学联赛山东省预赛
【标注】
【答案】
B
【解析】
如图，$O$ 是正三棱锥底面中心，也是半球的球心．$CD$ 是正三棱锥底面的高．侧面 $PAB$ 与半球相切于点 $E$，连结 $OE$，则$$OE\perp PD , OE=1 , PO=h.$$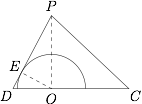
设 $\angle{PDO}=\alpha$（$0^{\circ}<\alpha <90^{\circ}$），则 $\angle{POE}=\alpha$，$h=\dfrac 1{\cos \alpha}$．
设正三棱锥底面三角形的边长为 $a$，则$$OD=\dfrac{\sqrt 3}{6}a=\dfrac 1{\sin \alpha},$$所以 $a=\dfrac{2\sqrt 3}{\sin \alpha}$．
正三棱锥的体积为$$V=\dfrac 13 \cdot \dfrac{\sqrt 3}{4}\cdot \left(\dfrac{2\sqrt 3}{\sin \alpha}\right)^2 \cdot \dfrac{1}{\cos \alpha}=\dfrac{\sqrt 3}{\sin ^2 \alpha\cos \alpha}.$$下面求体积的最小值．
令 $\cos \alpha =t$，则 $\sin ^2\alpha =1-t^2$，所以$$V=\dfrac{\sqrt 3}{(1-t^2)t}=\dfrac{\sqrt 3}{t-t^3},$$则$$V'=-\dfrac{\sqrt 3(1-3t^2)}{\left(t-t^3\right)^2}=\dfrac{\sqrt 3(3t^2-1)}{\left(t-t^3\right)^2}.$$已知 $0<t<1$，令 $V'<0$，得 $0<t<\dfrac{\sqrt 3}{3}$；令 $V'>0$，得 $\dfrac{\sqrt 3}{3}<t<1$．
因此当 $t=\dfrac{\sqrt 3}{3}$ 时，$$v_{\min}=\dfrac{\sqrt 3}{\dfrac{\sqrt 3}{3}-\left(\dfrac{\sqrt 3}{3}\right)^3}=\dfrac 92,$$相应的$$h=\dfrac 1{\cos \alpha}=\dfrac 1t =\sqrt 3.$$
设 $\angle{PDO}=\alpha$（$0^{\circ}<\alpha <90^{\circ}$），则 $\angle{POE}=\alpha$，$h=\dfrac 1{\cos \alpha}$．设正三棱锥底面三角形的边长为 $a$，则$$OD=\dfrac{\sqrt 3}{6}a=\dfrac 1{\sin \alpha},$$所以 $a=\dfrac{2\sqrt 3}{\sin \alpha}$．
正三棱锥的体积为$$V=\dfrac 13 \cdot \dfrac{\sqrt 3}{4}\cdot \left(\dfrac{2\sqrt 3}{\sin \alpha}\right)^2 \cdot \dfrac{1}{\cos \alpha}=\dfrac{\sqrt 3}{\sin ^2 \alpha\cos \alpha}.$$下面求体积的最小值．
令 $\cos \alpha =t$，则 $\sin ^2\alpha =1-t^2$，所以$$V=\dfrac{\sqrt 3}{(1-t^2)t}=\dfrac{\sqrt 3}{t-t^3},$$则$$V'=-\dfrac{\sqrt 3(1-3t^2)}{\left(t-t^3\right)^2}=\dfrac{\sqrt 3(3t^2-1)}{\left(t-t^3\right)^2}.$$已知 $0<t<1$，令 $V'<0$，得 $0<t<\dfrac{\sqrt 3}{3}$；令 $V'>0$，得 $\dfrac{\sqrt 3}{3}<t<1$．
因此当 $t=\dfrac{\sqrt 3}{3}$ 时，$$v_{\min}=\dfrac{\sqrt 3}{\dfrac{\sqrt 3}{3}-\left(\dfrac{\sqrt 3}{3}\right)^3}=\dfrac 92,$$相应的$$h=\dfrac 1{\cos \alpha}=\dfrac 1t =\sqrt 3.$$
题目
答案
解析
备注
