已知一个等边三角形的内接正方形面积为 $12$，则此等边三角形内接矩形面积的最大值为 ．
【难度】
【出处】
2017年北京大学物理秋令营基础学业能力数学测试
【标注】
【答案】
$\dfrac{7\sqrt 3}2+6$
【解析】
如图．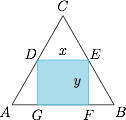
根据题意，等边三角形内接矩形的长宽分别为 $x,y$ 时，对应的等边三角形的边长为\[x+\dfrac{2y}{\sqrt 3}=2\sqrt 3+\dfrac {2\cdot 2\sqrt 3}{\sqrt 3}=4+2\sqrt 3,\]于是\[4+2\sqrt 3\geqslant 2\sqrt{\dfrac{2xy}{\sqrt 3}},\]从而内接矩形面积\[xy\leqslant (2+\sqrt 3)^2\cdot\dfrac{\sqrt 3}2=\dfrac{7\sqrt 3}2+6,\]等号当 $x=\dfrac{2y}{\sqrt 3}$ 时取得，因此所求的最大值为 $\dfrac{7\sqrt 3}2+6$．
根据题意，等边三角形内接矩形的长宽分别为 $x,y$ 时，对应的等边三角形的边长为\[x+\dfrac{2y}{\sqrt 3}=2\sqrt 3+\dfrac {2\cdot 2\sqrt 3}{\sqrt 3}=4+2\sqrt 3,\]于是\[4+2\sqrt 3\geqslant 2\sqrt{\dfrac{2xy}{\sqrt 3}},\]从而内接矩形面积\[xy\leqslant (2+\sqrt 3)^2\cdot\dfrac{\sqrt 3}2=\dfrac{7\sqrt 3}2+6,\]等号当 $x=\dfrac{2y}{\sqrt 3}$ 时取得，因此所求的最大值为 $\dfrac{7\sqrt 3}2+6$．
题目
答案
解析
备注
