查看数据源：5968850822d14000091d7253
正方体 $ABCD-A_1B_1C_1D_1$ 中 $BC_1$ 与截面 $BB_1D_1D$ 所成的角是  \((\qquad)\)
A: $\dfrac{\pi}{6}$
B: $\dfrac{\pi}{4}$
C: $\dfrac{\pi}{3}$
D: $\dfrac{\pi}{2}$
【难度】
【出处】
2012年全国高中数学联赛四川省预赛
【标注】
  • 数学竞赛
    >
    立体几何
    >
    空间计算
【答案】
A
【解析】
过 $C_1$ 作 $C_1O\perp B_1D_1$ 于点 $O$，连接 $BO$，则 $\angle C_1BO$ 即为所求的角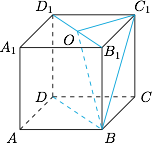．因为 $C_1O=\dfrac12BC_1$，所以 $\angle C_1BO=\dfrac{\pi}{6}$．
题目 答案 解析 备注
0.139472s