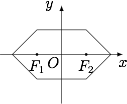
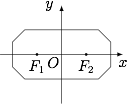
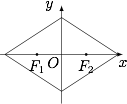
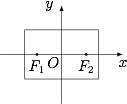
在平面直角坐标系中,两点 ${P_1}\left( {{x_1},{y_1}} \right),{P_2}\left( {{x_2},{y_2}} \right)$ 间的"L-距离"定义为 $|| {P_1}{P_2} ||= | {x_1} - {x_2} | + | {y_1} - {y_2} |$,则平面内与 $x$ 轴上两个不同的定点 ${F_1},{F_2}$ 的"L-距离"之和等于定值(大于 $| | {F_1}{F_2} ||$)的点的轨迹可以是 \((\qquad)\)
【难度】
【出处】
2014年高考福建卷(文)
【标注】
【答案】
A
【解析】
设 $F_1(-c,0)$,$F_2(c,0)$,$c>0$,轨迹上的任意一点 $M(x,y)$,则根据L-距离的定义,有$$|x+c|+|x-c|+2|y|=2a,$$不难得到在分区域讨论去掉绝对值符号后,方程总表现为直线方程,因此曲线由多段线段形成.而这些直线的斜率可能为 $0,1,-1$,即可得到答案.
题目
答案
解析
备注