设三角形 $ABC$ 的中线 $AL$ 与 $BM$ 相交于点 $K$，若 $K,L,C,M$ 四点共圆，则 $\dfrac{AB}{KC}$ 的值是 \((\qquad)\)
【难度】
【出处】
2016年北京大学生命科学冬令营试卷数学部分
【标注】
【答案】
C
【解析】
连结 $CK$ 并延长，使它交 $AB$ 边于点 $D$，连结 $LM$，交 $CD$ 于点 $E$，如图：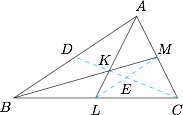
由题意知 $K$ 是 $\triangle ABC$ 的重心，所以 $D$ 为 $AB$ 的中点，$E$ 为 $CD$ 的中点，也为 $LM$ 的中点，且 $K$ 为 $CD$ 的靠近 $D$ 的三等分点．记 $KE=m$，则 $CD=6m,CE=3m$．
因为 $K,L,C,M$ 四点共圆，由相交弦定理知$$ME\cdot LE=KE\cdot CE=3m^2,$$解得 $ME=LE={\sqrt 3}m$．从而有$$\dfrac{AB}{KC}=\dfrac{2LM}{m+3m}=\dfrac{4\sqrt 3m}{4m}=\sqrt 3.$$
由题意知 $K$ 是 $\triangle ABC$ 的重心，所以 $D$ 为 $AB$ 的中点，$E$ 为 $CD$ 的中点，也为 $LM$ 的中点，且 $K$ 为 $CD$ 的靠近 $D$ 的三等分点．记 $KE=m$，则 $CD=6m,CE=3m$．因为 $K,L,C,M$ 四点共圆，由相交弦定理知$$ME\cdot LE=KE\cdot CE=3m^2,$$解得 $ME=LE={\sqrt 3}m$．从而有$$\dfrac{AB}{KC}=\dfrac{2LM}{m+3m}=\dfrac{4\sqrt 3m}{4m}=\sqrt 3.$$
题目
答案
解析
备注
