查看数据源：590a988f6cddca00092f6efa
点 $P$ 位于 $\triangle ABC$ 所在的平面内，使得 $\triangle PAB,\triangle PBC,\triangle PCA$ 的面积相等，则满足题意的点 $P$ 有 \((\qquad)\)
A: $1$ 个
B: $3$ 个
C: $5$ 个
D: 前三个答案都不对
【难度】
【出处】
2016年北京大学自主招生数学试题
【标注】
  • 题型
    >
    组合数学
    >
    组合计数
【答案】
D
【解析】
考虑到平面内使 $\triangle PAB$ 和 $\triangle PBC$ 的面积相等的点的轨迹为 $AC$ 边上中线所在的直线以及过点 $B$ 且与 $AC$ 平行的直线，其中 $M$ 为边 $AC$ 的中点，因此满足题意的点 $P$ 有 $4$ 个：$\triangle ABC$ 的重心，或者由 $P,A,B,C$ 四点所构成的平行四边形的顶点．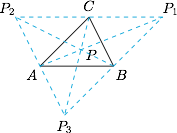
题目 答案 解析 备注
0.120140s