查看数据源：590ac8b36cddca00078f394c
设函数 $f(x)=\left(x^2-3\right){\rm e}^x$，则  \((\qquad)\)
A: $f(x)$ 有极小值，但无最小值
B: $f(x)$ 有极大值，但无最大值
C: 若方程 $f(x)=b$ 恰有一个实根，则 $b>\dfrac{6}{{\rm e}^3}$
D: 若方程 $f(x)=b$ 恰有三个不同实根，则 $0<b<\dfrac{6}{{\rm e}^3}$
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
    >
    利用导数研究函数的零点
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
【答案】
BD
【解析】
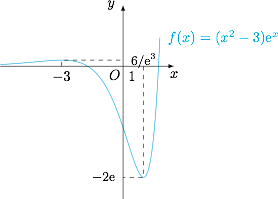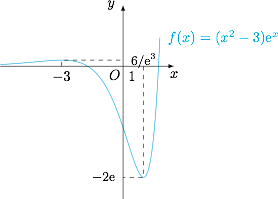函数 $f(x)$ 的导函数 $f'(x)={\rm e}^x\cdot\left(x^2+2x-3\right)$，可以画出函数草图如下：对于选项C，$b$ 的取值范围还应包含 $b=-2{\rm e}$．
题目 答案 解析 备注
0.112324s