在平面直角坐标系 $xOy$ 中，已知向量 $\overrightarrow a,\overrightarrow b$，$\left|\overrightarrow a\right|=\left|\overrightarrow b\right|=1$，$\overrightarrow a\cdot \overrightarrow b=0$，点 $Q$ 满足 $\overrightarrow{OQ}=\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)$，曲线$$C=\left\{P\left|\overrightarrow{OP}=\cos\theta\overrightarrow a+\sin\theta\overrightarrow b,0\leqslant \theta<2\pi\right.\right\},$$区域$$\Omega=\left\{P\left|0<r\leqslant \left|\overrightarrow{PQ}\right|\leqslant R,r<R\right.\right\}.$$若 $C\cap \Omega$ 为两段分离的曲线，则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
注意到\[\overrightarrow{OQ}\cdot\overrightarrow{OQ}=\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)\cdot\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)=2\left|\overrightarrow a\right|^2+2\left|\overrightarrow b\right|^2=4,\]于是 $Q$ 在以 $O$ 为圆心，$2$ 为半径的圆上．
另一方面，类似可得\[\begin{split}\overrightarrow{OP}\cdot\overrightarrow{OP}&=\left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\cdot \left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\\&=\cos^2\theta\left|\overrightarrow a\right|^2+\sin^2\theta\left|\overrightarrow b\right|^2=1,\end{split}\]于是曲线 $C$ 是以 $O$ 为圆心，$1$ 为半径的圆．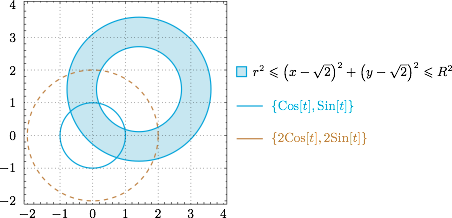
据此，我们可以画出示意图，题意即圆心在虚圆上的圆环（“和氏璧”）截实圆为两段分离的弧，于是 $r>1\land R<3$，选项 A 符合题意．
另一方面，类似可得\[\begin{split}\overrightarrow{OP}\cdot\overrightarrow{OP}&=\left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\cdot \left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\\&=\cos^2\theta\left|\overrightarrow a\right|^2+\sin^2\theta\left|\overrightarrow b\right|^2=1,\end{split}\]于是曲线 $C$ 是以 $O$ 为圆心，$1$ 为半径的圆．
据此，我们可以画出示意图，题意即圆心在虚圆上的圆环（“和氏璧”）截实圆为两段分离的弧，于是 $r>1\land R<3$，选项 A 符合题意．
题目
答案
解析
备注
