查看数据源：590acb746cddca00078f3965
设不等式组 $\begin{cases} |x|+|y|\leqslant 2,\\ y+2\leqslant k(x+1),\end{cases}$ 所表示的区域为 $D$，其面积为 $S$，则  \((\qquad)\)
A: 若 $S=4$，则 $k$ 的值唯一
B: 若 $S=\dfrac 12$，则 $k$ 的值有 $2$ 个
C: 若 $D$ 为三角形，则 $0<k\leqslant \dfrac 23$
D: 若 $D$ 为五边形，则 $k>4$
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
  • 方法
    >
    数形结合
    >
    不等式(组)的规划
  • 知识点
    >
    解析几何
    >
    直线
    >
    直线的方程
    >
    直线的点斜式方程
【答案】
ABD
【解析】
如图，随着 $k$ 的不同，区域形状随之变化．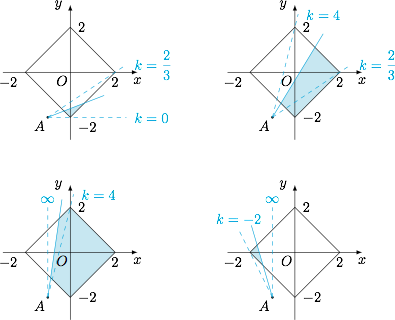
题目 答案 解析 备注
0.287656s