查看数据源：590ad07c6cddca000a081a26
设非负实数 $x,y$ 满足 $2x+y=1$，则 $x+\sqrt{x^2+y^2}$ 的 \((\qquad)\)
A: 最小值为 $\dfrac 45$
B: 最小值为 $\dfrac 25$
C: 最大值为 $1$
D: 最大值为 $\dfrac{1+\sqrt 2}3$
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
  • 方法
    >
    数形结合
    >
    转化为距离
  • 题型
    >
    不等式
    >
    求代数式的最值与范围
【答案】
AC
【解析】
设 $P$ 在 $y$ 轴上的投影为 $H$，则$$x+\sqrt{x^2+y^2}=PO+PH,$$如图．作原点 $O$ 关于直线 $2x+y=1$ 的对称点 $O'\left(\dfrac 45,\dfrac 25\right)$，则 $PO+PH=O'P+PH$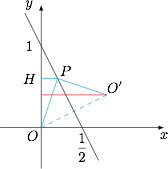．由图不难得到 $O'P+PH$ 的最小值为 $\dfrac 45$，而最大值为 $1$．
题目 答案 解析 备注
0.176165s