如图，$\triangle ABC$ 中，$\angle BAC=90^\circ$，$AB=3$，$AC=4$，点 $D$ 是 $BC$ 的中点，将 $\triangle ABD$ 沿 $AD$ 翻折得到 $\triangle AED$，连接 $CE$，则线段 $CE$ 的长等于 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
连接 $BE$ 交 $AD$ 于点 $F$．
由翻折可得 $DE=DB$，$AD\perp BE$，$BE=2BF$．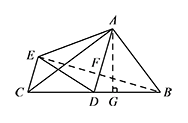
由点 $D$ 为 $BC$ 中点，$\angle BAC=90^\circ$，
所以 $DE=DB=DC=DA$，
从而 $\angle BEC=90^\circ$．
过点 $A$ 作 $AG\perp BC$ 于点 $G$，则 $AG\cdot BC=AB\cdot AC$．
而 $AB=3,AC=4$，所以 $BC=5$，
从而 $AG=\dfrac{12}5$．
易证 $\triangle AGD\cong \triangle BFD$，
所以 $BF=\dfrac{12}5$，$BE=\dfrac{24}5$．
所以在 $\triangle BEC$ 中，$CE=\sqrt{BC^2-BE^2}=\dfrac 75$．
由翻折可得 $DE=DB$，$AD\perp BE$，$BE=2BF$．
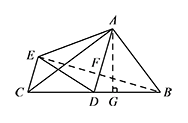由点 $D$ 为 $BC$ 中点，$\angle BAC=90^\circ$，所以 $DE=DB=DC=DA$，
从而 $\angle BEC=90^\circ$．
过点 $A$ 作 $AG\perp BC$ 于点 $G$，则 $AG\cdot BC=AB\cdot AC$．
而 $AB=3,AC=4$，所以 $BC=5$，
从而 $AG=\dfrac{12}5$．
易证 $\triangle AGD\cong \triangle BFD$，
所以 $BF=\dfrac{12}5$，$BE=\dfrac{24}5$．
所以在 $\triangle BEC$ 中，$CE=\sqrt{BC^2-BE^2}=\dfrac 75$．
题目
答案
解析
备注
