设函数 $y=f(x)$ 的图象与 $y=2^{x+a}$ 的图象关于直线 $y=-x$ 对称，且 $f(-2)+f(-4)=1$，则 $a=$ \((\qquad)\)
【难度】
【出处】
2015年高考全国Ⅰ卷（文）
【标注】
【答案】
C
【解析】
一个点关于直线 $y=-x$ 的对称点可以看作是先关于直线 $y=x$ 对称，再关于原点对称的结果，如图．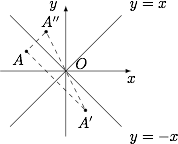
于是函数 $y=f(x)$ 的解析式等价于$$-x=2^{-y+a},$$即$$y=a-{\log_2}{(-x)}.$$根据题意，有$$a-{\log_2}{(-(-2))}+a-{\log_2}{(-(-4))}=1,$$解得 $a=2$．
于是函数 $y=f(x)$ 的解析式等价于$$-x=2^{-y+a},$$即$$y=a-{\log_2}{(-x)}.$$根据题意，有$$a-{\log_2}{(-(-2))}+a-{\log_2}{(-(-4))}=1,$$解得 $a=2$．
题目
答案
解析
备注
