查看数据源：59102faf40fdc7000a51cf7d
点 $P$ 在直线 $l$：$y=x-1$ 上，若存在过 $P$ 的直线交抛物线 $y=x^2$ 于 $A,B$ 两点，且 $|PA|=|AB|$，则称点 $P$ 为“$A$ 点”，那么下列结论中正确的是 \((\qquad)\)
A: 直线 $l$ 上的所有点都是“$A$ 点”
B: 直线 $l$ 上仅有有限个点是“$A$ 点”
C: 直线 $l$ 上的所有点都不是“$A$ 点”
D: 直线 $l$ 上有无穷多点（但不是所有点）是“$A$ 点”
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
点 $P$ 形成的轨迹为抛物线的外部，示意图如下：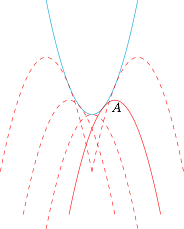
题目 答案 解析 备注
0.110019s