设函数 $f'(x)$ 是奇函数 $f(x)$（$x\in\mathbb R$）的导函数，$f(-1)=0$，当 $x>0$ 时，$xf'(x)-f(x)<0$，则使得 $f(x)>0$ 成立的 $x$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2015年高考全国II卷（理）
【标注】
【答案】
A
【解析】
注意到核心条件：当 $x>0$ 时，$xf'(x)-f(x)<0$，即$$x^2\cdot\left(x^{-1}\cdot f(x)\right)'<0,$$于是可设辅助函数$$g(x)=x^{-1}\cdot f(x),x\neq 0.$$根据题意，该函数为偶函数，$g(-1)=0$，且在 $(0,+\infty)$ 上单调递减，如图．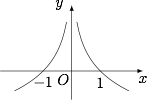
不等式 $f(x)>0$，即$$x\cdot g(x)>0,$$因此解集为 $(-\infty,-1)\cup (0,1)$．
不等式 $f(x)>0$，即$$x\cdot g(x)>0,$$因此解集为 $(-\infty,-1)\cup (0,1)$．
题目
答案
解析
备注
