锐角 $\triangle ABC$ 内接于 $ \odot O$，$O$ 到 $a , b, c$ 三边的距离分别为 $k, m , n$，则 $k:m:n = $ \((\qquad)\)
【难度】
【出处】
2012年北京大学等十三校联考自主招生
【标注】
【答案】
D
【解析】
如图．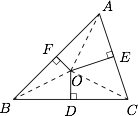
有\[\begin{split}OD:OE:OF&= \dfrac{{{S_{\triangle OBC}}}}{{BC}}:\dfrac{{{S_{\triangle OCA}}}}{{CA}}:\dfrac{{{S_{\triangle OAB}}}}{{AB}}\\&= \dfrac{{\dfrac{1}{2}\sin 2A}}{{BC}}:\dfrac{{\dfrac{1}{2}\sin 2B}}{{CA}}:\dfrac{{\dfrac{1}{2}\sin 2C}}{{AB}}\\& = \cos A:\cos B:\cos C.\end{split}\]
有\[\begin{split}OD:OE:OF&= \dfrac{{{S_{\triangle OBC}}}}{{BC}}:\dfrac{{{S_{\triangle OCA}}}}{{CA}}:\dfrac{{{S_{\triangle OAB}}}}{{AB}}\\&= \dfrac{{\dfrac{1}{2}\sin 2A}}{{BC}}:\dfrac{{\dfrac{1}{2}\sin 2B}}{{CA}}:\dfrac{{\dfrac{1}{2}\sin 2C}}{{AB}}\\& = \cos A:\cos B:\cos C.\end{split}\]
题目
答案
解析
备注
