点 $C$ 在圆 ${x^2} + {y^2} - 2x = 0$ 上，$A$ 点坐标为 $\left( { - 2, 0} \right)$，$B$ 点坐标为 $\left( {0, 2} \right)$，则 $\triangle ABC$ 面积的最小值为 \((\qquad)\)
【难度】
【出处】
2012年北京大学等十三校联考自主招生
【标注】
【答案】
A
【解析】
圆即 ${\left( {x - 1} \right)^2} + {y^2} = 1$，所以，圆心 $\left( {1 ,0} \right)$ 到直线 $AB:x - y + 2 = 0$ 的距离为 $\dfrac{3}{{\sqrt 2 }}$．
如图，以 $AB$ 为底边，$\triangle ABC$ 的高的最小值为 $\dfrac{3}{{\sqrt 2 }} - 1$．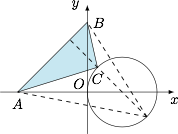
因此 ${S_{\triangle ABC}}$ 的最小值为$$\dfrac{1}{2} \cdot 2\sqrt 2 \cdot \left( {\dfrac{3}{{\sqrt 2 }} - 1} \right) = 3 - \sqrt 2 .$$
如图，以 $AB$ 为底边，$\triangle ABC$ 的高的最小值为 $\dfrac{3}{{\sqrt 2 }} - 1$．
因此 ${S_{\triangle ABC}}$ 的最小值为$$\dfrac{1}{2} \cdot 2\sqrt 2 \cdot \left( {\dfrac{3}{{\sqrt 2 }} - 1} \right) = 3 - \sqrt 2 .$$
题目
答案
解析
备注
