先画出示意图，设 $A,B,C$ 点的横坐标分别为 $t-m,t,t+m$，不妨设 $m>0$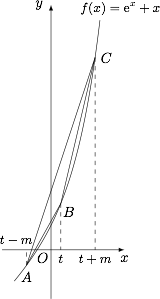．命题 ① 与 ② 互斥，命题 ③ 与 ④ 互斥，我们分别考虑．
对于命题 ①②，需要考虑 $\triangle ABC$ 的最大角．由示意图，猜测 $B$ 为最大角．论证如下：
$B$ 为最大角
$\Leftarrow AC$ 为最大边
$\Leftarrow AC>AB$，$AC>BC$
$\Leftarrow |x_A-x_C|>|x_B-x_A|=|x_C-x_B|$
而 $|y_C-y_A|=|y_C-y_B|+|y_B-y_A|$（$f(x)$ 为单调递增函数）．
接下来如果利用余弦定理去判断 $AB^2+BC^2-AC^2$ 的正负计算量比较大，认真观察示意图不难发现 $AB$ 的斜率$$k_{AB}=\dfrac {\left({\mathrm e}^{t}+t\right)-\left({\mathrm e}^{t-m}+t-m\right)}{t-\left(t-m\right)}=\dfrac {{\mathrm e}^{t}-{\mathrm e}^{t-m}+m}{m}>0.$$同理 $BC$ 的斜率也大于 $0$．
因此 $\overrightarrow {AB}$ 与 $\overrightarrow {BC}$ 的夹角即 $B$ 的补角为锐角，从而 $B$ 一定为钝角．
从而命题 ① 正确．
进而考虑命题 ③④．
我们已经知道 $AC>AB$，$AC>BC$，于是 $\triangle ABC$ 是等腰三角形的唯一希望就是 $AB=BC$ 了．
由示意图，答案应该是否定的．因为根据示意图，可猜测 $BC$ 的斜率大于 $AB$ 的斜率，这样就有 $BC=\sqrt {1+k_{BC}^2}\cdot m>\sqrt {1+k_{AB}^2}\cdot m=AB$ 了．论证如下：
因为 $k_{AB}=\dfrac {{\mathrm e}^{t}-{\mathrm e}^{t-m}}{m}+1$，$k_{BC}=\dfrac {{\mathrm e}^{t+m}-{\mathrm e}^{t}}{m}+1$，
所以$$k_{BC}>k_{AB} \Leftarrow {\mathrm e}^{t+m}-{\mathrm e}^{t}>{\mathrm e}^{t}-{\mathrm e}^{t-m} \Leftarrow {\mathrm e}^{t+m}+{\mathrm e}^{t-m}>2{\mathrm e}^{t}.$$由均值不等式及其等号取得的条件，上式成立．
从而命题 ④ 正确．
综上，选B．