查看数据源：5910081d857b42000aca3922
在半径为 $1$ 的圆周上随机选取 $3$ 点，它们构成一个锐角三角形的概率是 \((\qquad)\)
A: $\dfrac{1}{2}$
B: $\dfrac{1}{3}$
C: $\dfrac{1}{4}$
D: $\dfrac{1}{5}$
【难度】
【出处】
2011年复旦大学优秀高中生文化水平选拔测试
【标注】
  • 知识点
    >
    计数与概率
    >
    随机事件的概率
    >
    几何概型
  • 方法
    >
    数形结合
    >
    不等式(组)的规划
【答案】
C
【解析】
设三个点 $A$、$B$、$C$ 把圆周分为 $x$、$y$、${\mathrm {2\pi }} - \left( {x + y} \right)$ 三段，则样本空间为$$\begin{cases}
x > 0 ,\\
y > 0 ,\\
{\mathrm {2\pi }} - \left( {x + y} \right) > 0 .\\
\end{cases}$$即$$\begin{cases}x > 0 ,\\
y > 0 ,\\
x + y < 2{\mathrm {\pi }} .\\
\end{cases}$$$\triangle ABC$ 为锐角三角形的充要条件为$$\begin{cases}0 < x < {\mathrm {\pi }},\\
0 < y < {\mathrm {\pi }} ,\\
0 < 2{\mathrm {\pi }} - \left( {x + y} \right) < {\mathrm {\pi }}.\\
\end{cases}$$即$$\begin{cases}0 < x < {\mathrm {\pi }} ,\\
0 < y < {\mathrm {\pi }},\\
x + y > {\mathrm {\pi }}.\\
\end{cases}$$如图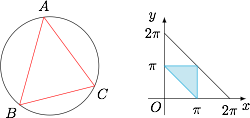：所求概率为 $\dfrac{1}{4}$．
题目 答案 解析 备注
0.117787s