已知 $f(x)$ 是定义在 $\mathbb R$ 上以 $2$ 为周期的偶函数．当 $0\leqslant x\leqslant 1$ 时，$f(x)=x^2$，若直线 $y=\dfrac 12x+a$ 与 $y=f(x)$ 的图象恰有两个公共点，则 \((\qquad)\)
【难度】
【出处】
2009年全国高中数学联赛新疆维吾尔自治区预赛
【标注】
【答案】
C
【解析】
易知当 $-1\leqslant x\leqslant 1$ 时，$f(x)=x^2$．
当直线过点 $(1,1)$ 时，$a=\dfrac 12$．
当直线与 $f(x)=x^2$ 的图象相切时，由$$\begin{cases}y=x^2,\\ y=\dfrac 12 x+a,\end{cases}$$得$$x^2-\dfrac 12 x-a=0,$$所以$$\Delta =\dfrac 14 +4a=0,$$解得 $a=-\dfrac 1{16}$，此时直线与 $y=f(x)$ 的图象恰有两个交点．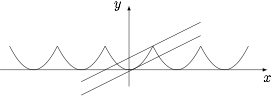
由周期性知，若直线 $y=\dfrac 12 x+a$ 满足，则 $y=\dfrac 12(x+2k)+a$ 也满足，所以 $a=\dfrac 12+k$ 或 $a=k-\dfrac 1{16}$（$k\in \mathbb Z$）．
当直线过点 $(1,1)$ 时，$a=\dfrac 12$．
当直线与 $f(x)=x^2$ 的图象相切时，由$$\begin{cases}y=x^2,\\ y=\dfrac 12 x+a,\end{cases}$$得$$x^2-\dfrac 12 x-a=0,$$所以$$\Delta =\dfrac 14 +4a=0,$$解得 $a=-\dfrac 1{16}$，此时直线与 $y=f(x)$ 的图象恰有两个交点．
由周期性知，若直线 $y=\dfrac 12 x+a$ 满足，则 $y=\dfrac 12(x+2k)+a$ 也满足，所以 $a=\dfrac 12+k$ 或 $a=k-\dfrac 1{16}$（$k\in \mathbb Z$）．
题目
答案
解析
备注
