在正四棱锥 $P - ABCD$ 中，$M,N$ 分别为 $PA,PB$ 的中点，且侧面与底面所成二面角的正切为 $\sqrt 2 $，则异面直线 $DM$ 与 $AN$ 所成角的余弦为 \((\qquad)\)
【难度】
【出处】
2011年清华大学等七校联考自主招生试题
【标注】
【答案】
D
【解析】
如左图，取 $PN$ 的中点 $E$，连结 $ME$、$DE$，则 $ME\parallel AN$，于是 $\left| {\cos \angle DME} \right|$ 为所求．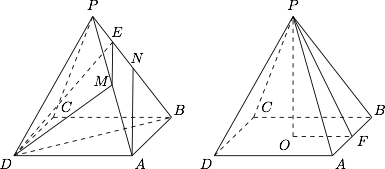
如右图，$\dfrac{{PO}}{{OF}} = \sqrt 2 $，于是取 $OF = 1$，$PO = \sqrt 2 $，则正方形 $ABCD$ 的边长为 $2$．
于是$$PB = \sqrt {P{O^2} + {{\left( {\frac{{\sqrt 2 }}{2}AB} \right)}^2}} = \sqrt {2 + 2} = 2,$$因此 $\triangle PAD$ 是等边三角形，$DM = \sqrt 3$，所以$$ME = \dfrac{1}{2}AN = \dfrac{1}{2}DM = \dfrac{{\sqrt 3 }}{2},$$而 $\triangle PBD$ 为等腰直角三角形，$\angle BPD$ 为直角，而 $PE = \dfrac{1}{4}PB = \dfrac{1}{2}$，所以$$DE = \sqrt {P{D^2} + P{E^2}} = \sqrt {4 + \dfrac{1}{4}} = \dfrac{{\sqrt {17} }}{2},$$于是在 $\triangle DME$ 中，$\cos \angle DME$ $=-\dfrac{1}{6} $，因此，所成角的余弦值为 $ \dfrac{1}{6}$．
如右图，$\dfrac{{PO}}{{OF}} = \sqrt 2 $，于是取 $OF = 1$，$PO = \sqrt 2 $，则正方形 $ABCD$ 的边长为 $2$．于是$$PB = \sqrt {P{O^2} + {{\left( {\frac{{\sqrt 2 }}{2}AB} \right)}^2}} = \sqrt {2 + 2} = 2,$$因此 $\triangle PAD$ 是等边三角形，$DM = \sqrt 3$，所以$$ME = \dfrac{1}{2}AN = \dfrac{1}{2}DM = \dfrac{{\sqrt 3 }}{2},$$而 $\triangle PBD$ 为等腰直角三角形，$\angle BPD$ 为直角，而 $PE = \dfrac{1}{4}PB = \dfrac{1}{2}$，所以$$DE = \sqrt {P{D^2} + P{E^2}} = \sqrt {4 + \dfrac{1}{4}} = \dfrac{{\sqrt {17} }}{2},$$于是在 $\triangle DME$ 中，$\cos \angle DME$ $=-\dfrac{1}{6} $，因此，所成角的余弦值为 $ \dfrac{1}{6}$．
题目
答案
解析
备注
