$l$ 和 $l'$ 是互相垂直的异面直线,$l$ 与平面 $\pi$ 平行,$l'$ 在平面 $\pi$ 内.在平面 $\pi$ 内到 $l$ 和 $l'$ 距离相等的点的轨迹是 \((\qquad)\)
【难度】
【出处】
2011年全国高中数学联赛辽宁省预赛
【标注】
【答案】
D
【解析】
在平面 $\pi$ 内以 $l'$ 为 $x$ 轴,以 $l$ 在平面 $\pi$ 内的投影(过 $l$ 垂直于 $\pi$ 的平面与 $\pi$ 的交线)为 $y$ 轴建立直角坐标系,则平面 $\pi$ 内动点 $M(x,y)$ 到 $l'$ 的距离为 $|y|$,到 $l$ 的距离为 $\sqrt{x^2+a^2}$,于是$$|y|=\sqrt{x^2+a^2},$$即$$y^2-x^2=a^2$$(其中 $a$ 是异面直线 $l$ 和 $l'$ 的距离).
因此,所求轨迹是双曲线.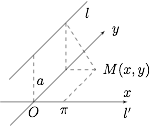
因此,所求轨迹是双曲线.

题目
答案
解析
备注