查看数据源：596317633cafba000761310a
正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，在侧面对角线 $A_1D$ 上取点 $M$，$CD_1$ 上取点 $N$，使得线段 $MN$ 平行于对角面 $A_1ACC_1$，则这样的 $MN$ 长度最小值为 \((\qquad)\)
A: $\dfrac {\sqrt 3}{3}$
B: $\dfrac{\sqrt 2}{2}$
C: $1$
D: $\sqrt 2$
【难度】
【出处】
2011年全国高中数学联赛辽宁省预赛
【标注】
【答案】
A
【解析】
作 $MM_1\perp AD$ 于 $M_1$，$NN_1\perp DC$ 于 $N_1$，易证$$M_1N_1\parallel AC.$$设 $DM_1=DN_1=x$，则$$MM_1=x,NN_1=1-x.$$过 $M$ 作 $MH\perp NN_1$ 于 $H$，则$$NH=1-2x,M_1N_1=\sqrt 2 x.$$由勾股定理\[\begin{split}MN^2&=(\sqrt 2x)^2+(1-2x)^2\\&=6\left(x-\dfrac 13\right)^2+\dfrac 13,\end{split}\]当 $x=\dfrac 13$ 时，$MN$ 取到最小值 $\dfrac {\sqrt 3}{3}$．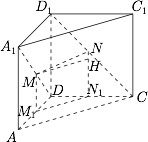
题目 答案 解析 备注
0.117558s