查看数据源：59631eee3cafba0008337319
若点 $P$ 在曲线 $y=-x^2-1$ 上，点 $Q$ 在曲线 $x=1+y^2$ 上，则 $|PQ|$ 的最小值是 \((\qquad)\)
A: $3\sqrt 2$
B: $\dfrac{3\sqrt 2}{2}$
C: $\dfrac{3\sqrt 2}{4}$
D: $\dfrac{3\sqrt 2}{8}$
【难度】
【出处】
2011年全国高中数学联赛山东省预赛
【标注】
【答案】
C
【解析】
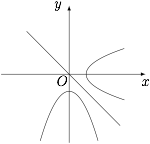因为两抛物线 $y=-x^2-1$，$x=1+y^2$ 关于直线 $y=-x$ 对称，所以所求 $|PQ|$ 的最小值为抛物线 $y=-x^2-1$ 上的点到直线 $y=-x$ 距离的最小值的两倍．
设 $P(x,-x^2-1)$ 为 $y=-x^2-1$ 上任意点，则$$d=\dfrac{|x-x^2-1|}{\sqrt 2}=\dfrac{x^2-x+1}{\sqrt 2},$$所以$$d_{\min}=\dfrac{3\sqrt 2}{8},|PQ|_{\min}=\dfrac{3\sqrt 2}{4}.$$
题目 答案 解析 备注
0.117598s