如图，边长为 $2$ 的正方形 $ABCD$ 和正方形 $ABEF$ 所在的面成 $60^{\circ}$ 角，$M,N$ 分别是线段 $AC$ 和 $BF$ 上的点，且 $AM=FN$，则线段 $MN$ 的长的取值范围是 \((\qquad)\) 
【难度】
【出处】
2011年全国高中数学联赛四川省预赛
【标注】
【答案】
B
【解析】
过点 $M$ 作 $MH\parallel BC$ 交 $AB$ 于 $H$，则$$\dfrac{AM}{AC}=\dfrac{AH}{AB},$$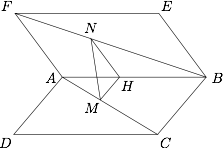
又 $AM=FN$，$AC=FB$，
所以$$\dfrac{FN}{FB}=\dfrac{AH}{AB},$$故$$NH\parallel AF,NH\perp AB,MH\perp AB,$$所以 $\angle{MHN}=60^{\circ}$．
设 $AH=x(0\leqslant x\leqslant 2)$，则 $MH=x$，$NH=2-x$，所以\[\begin{split}MN&=\sqrt{x^2+(2-x)^2-2x(2-x)\cos{60^{\circ}}}\\&=\sqrt{3x^2-6x+4}\\&=\sqrt{3(x-1)^2+1}.\end{split}\]因此 $1\leqslant MN\leqslant 2$．
又 $AM=FN$，$AC=FB$，所以$$\dfrac{FN}{FB}=\dfrac{AH}{AB},$$故$$NH\parallel AF,NH\perp AB,MH\perp AB,$$所以 $\angle{MHN}=60^{\circ}$．
设 $AH=x(0\leqslant x\leqslant 2)$，则 $MH=x$，$NH=2-x$，所以\[\begin{split}MN&=\sqrt{x^2+(2-x)^2-2x(2-x)\cos{60^{\circ}}}\\&=\sqrt{3x^2-6x+4}\\&=\sqrt{3(x-1)^2+1}.\end{split}\]因此 $1\leqslant MN\leqslant 2$．
题目
答案
解析
备注
