查看数据源：59110dc540fdc70009113e25
在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$E$ 为棱 $A{A_1}$ 的中点，$F$ 是棱 ${A_1}{B_1}$ 上的点，且 ${A_1}F:F{B_1} = 1:3$，则异面直线 $EF$ 与 $B{C_1}$ 所成角的正弦值为 \((\qquad)\)
A: $\dfrac{{\sqrt {15} }}{3}$
B: $\dfrac{{\sqrt {15} }}{5}$
C: $\dfrac{{\sqrt 5 }}{3}$
D: $\dfrac{{\sqrt 5 }}{5}$
【难度】
【出处】
2011年清华大学夏令营试题
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    异面直线所成的角
【答案】
B
【解析】
如图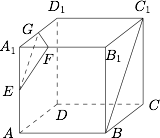．记正方体棱长为 $4$，则$$EF=GF=\sqrt{5},EG=2\sqrt 2,$$于是有$$\sin\angle FEG=\dfrac{\sqrt{5-2}}{\sqrt{5}}=\dfrac {\sqrt{15}}{5}.$$
题目 答案 解析 备注
0.118248s