在直三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，底面边长与侧棱长均等于 $2$，且 $E$ 为 $C{C_1}$ 的中点，则点 ${C_1}$ 到平面 $A{B_1}E$ 的距离为 \((\qquad)\)
【难度】
【出处】
2011年清华大学夏令营试题
【标注】
【答案】
D
【解析】
如图，用体积法．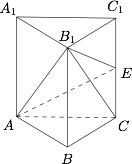
因为 $A{B_1} = 2\sqrt 2 $，${B_1}E = \sqrt 5 $，$AE = \sqrt 5 $，所以 ${S_{\triangle A{B_1}E}} = \sqrt 6 $．
因此$$\dfrac{{d\left( {{C_1},A{B_1}E} \right)}}{{d\left( {{B_1},AEC} \right)}} = \dfrac{{{S_{\triangle AEC}}}}{{{S_{\triangle A{B_1}E}}}} = \dfrac{1}{{\sqrt 6 }},$$所求距离为 $\dfrac{1}{{\sqrt 6 }} \cdot \sqrt 3 = \dfrac{{\sqrt 2 }}{2}$．
因为 $A{B_1} = 2\sqrt 2 $，${B_1}E = \sqrt 5 $，$AE = \sqrt 5 $，所以 ${S_{\triangle A{B_1}E}} = \sqrt 6 $．因此$$\dfrac{{d\left( {{C_1},A{B_1}E} \right)}}{{d\left( {{B_1},AEC} \right)}} = \dfrac{{{S_{\triangle AEC}}}}{{{S_{\triangle A{B_1}E}}}} = \dfrac{1}{{\sqrt 6 }},$$所求距离为 $\dfrac{1}{{\sqrt 6 }} \cdot \sqrt 3 = \dfrac{{\sqrt 2 }}{2}$．
题目
答案
解析
备注
