查看数据源：59110e2940fdc70009113e2b
若关于 $x$ 的方程 $\dfrac{{|x|}}{{x + 4}} = k{x^2}$ 有四个不同的实数解，则 $k$ 的取值范围为  \((\qquad)\)
A: $\left( {0,1} \right)$
B: $\left( {\dfrac{1}{4},1} \right)$
C: $\left( {\dfrac{1}{4},+ \infty } \right)$
D: $\left( {1,+ \infty } \right)$
【难度】
【出处】
2011年清华大学夏令营试题
【标注】
  • 方法
    >
    代数处理
    >
    分离变量法
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
【答案】
C
【解析】
$x=0$ 是方程的解．当 $x\ne 0$ 时，方程等价于\[\dfrac 1k=\dfrac{x}{|x|}\cdot x(x+4),\]如图，有 $\dfrac 1k\in(0,4)$，从而有 $k\in\left(\dfrac 14,+\infty\right)$．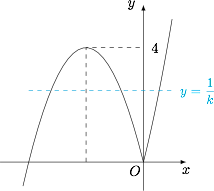
题目 答案 解析 备注
0.242931s