设 $\sigma $ 是坐标平面按顺时针方向绕原点做角度为 $\dfrac{{2{{\pi }}}}{7}$ 的旋转，$\tau $ 表示坐标平面关于 $y$ 轴的镜面反射，用 $\tau \sigma $ 表示变换的复合，先做 $\tau $，再做 $\sigma $，用 ${\sigma ^k}$ 表示连续 $k$ 次 $\sigma $ 的变换，则 $\sigma \tau {\sigma ^2}\tau {\sigma ^3}\tau {\sigma ^4}$ 是 \((\qquad)\)
【难度】
【出处】
2011年卓越联盟（同济等九校）自主招生联考数学试题
【标注】
【答案】
D
【解析】
如图 ${\sigma ^4}\left( 0 \right) = 8$，${\sigma ^5}\left( 0 \right) = 10$，${\sigma ^2}\tau \left( 0 \right) = 3$，$\tau {\sigma ^2}\left( 0 \right) = 11$．
而$$\sigma \tau {\sigma ^2}\tau {\sigma ^3}\tau {\sigma ^4}\left( 0 \right) = {\sigma ^2}\tau {\sigma ^3}\tau {\sigma ^4}\left( 5 \right) = {\sigma ^3}\tau {\sigma ^4}\left( {12} \right) = {\sigma ^4}\left( 3 \right) = 11.$$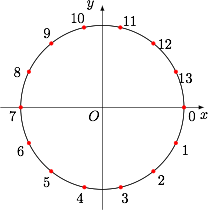
或用复数的三角形式，$\sigma \left( \theta \right) = \theta - \dfrac{{2{{\pi }}}}{7}$；$\tau \left( \theta \right) = {{\pi }} - \theta $．
而$$\sigma \tau {\sigma ^2}\tau {\sigma ^3}\tau {\sigma ^4}\left( 0 \right) = {\sigma ^2}\tau {\sigma ^3}\tau {\sigma ^4}\left( 5 \right) = {\sigma ^3}\tau {\sigma ^4}\left( {12} \right) = {\sigma ^4}\left( 3 \right) = 11.$$
或用复数的三角形式，$\sigma \left( \theta \right) = \theta - \dfrac{{2{{\pi }}}}{7}$；$\tau \left( \theta \right) = {{\pi }} - \theta $．
题目
答案
解析
备注
