设直线 $l$ 与球 $O$ 有且只有一个公共点 $P$，从直线 $l$ 出发的两个半平面 $\alpha$，$\beta$ 截球 $O$ 的两个截面圆的半径分别为 $1$ 和 $\sqrt 3$，二面角 $\alpha -l-\beta$ 的平面角为 $\dfrac {5\pi}{ 6}$，则球 $O$ 的半径为 \((\qquad)\)
【难度】
【出处】
2014年全国高中数学联赛辽宁省预赛
【标注】
【答案】
B
【解析】
由题意及球的对称性可得图形的剖面图如图所示，$O_1P$，$O_2P$ 分别为两圆形平面的半径．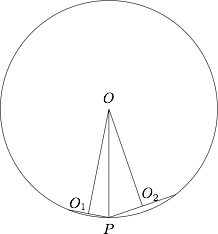
设 $O_1P=1$，$O_2P=\sqrt 3$，$O_1O=d_1$，$O_2O=d_2$，球的半径为 $R$．
由题意及余弦定理可得$$\begin{cases}d_1^2+1=d_2^2+3=R^2,\\ d_1^2+d_2^2-2d_1d_2\cos \dfrac {\pi}{6}=1+3-2\sqrt 3 \cos \dfrac {5\pi}{6},\end{cases}$$解得$$\begin{cases}d_1^2=27,\\ d_2^2=25,\\R^2=28,\end{cases}$$因此球的半径 $R=2\sqrt 7$．
设 $O_1P=1$，$O_2P=\sqrt 3$，$O_1O=d_1$，$O_2O=d_2$，球的半径为 $R$．由题意及余弦定理可得$$\begin{cases}d_1^2+1=d_2^2+3=R^2,\\ d_1^2+d_2^2-2d_1d_2\cos \dfrac {\pi}{6}=1+3-2\sqrt 3 \cos \dfrac {5\pi}{6},\end{cases}$$解得$$\begin{cases}d_1^2=27,\\ d_2^2=25,\\R^2=28,\end{cases}$$因此球的半径 $R=2\sqrt 7$．
题目
答案
解析
备注
