已知函数 $f\left(x\right)=\begin{cases}
2- \left|x \right|,&x\leqslant 2, \\ \left(x-2\right)^2,&x>2,
\end{cases}$ 函数 $g\left(x\right)=3-f\left(2-x\right)$,则函数 $y=f\left(x\right)-g\left(x\right)$ 的零点个数为 \((\qquad)\)
2- \left|x \right|,&x\leqslant 2, \\ \left(x-2\right)^2,&x>2,
\end{cases}$ 函数 $g\left(x\right)=3-f\left(2-x\right)$,则函数 $y=f\left(x\right)-g\left(x\right)$ 的零点个数为 \((\qquad)\)
【难度】
【出处】
2015年高考天津卷(文)
【标注】
【答案】
A
【解析】
函数 $g(x)$ 与 $f(x)$ 的图象关于点 $\left(1,\dfrac 32\right)$ 中以对称,如图: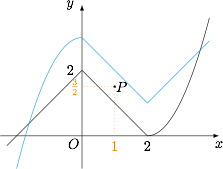

题目
答案
解析
备注