已知常数 ${k_1}$、${k_2}$ 满足 $0 < {k_1} < {k_2}$，${k_1}{k_2} = 1$．设 ${C_1}$ 和 ${C_2}$ 分别是以 $y = \pm {k_1}\left( {x - 1} \right) + 1$ 和 $y = \pm {k_2}\left( {x - 1} \right) + 1$ 为渐近线且通过原点的双曲线，则 ${C_1}$ 和 ${C_2}$ 的离心率之比 $\dfrac{{{e_1}}}{{{e_2}}}$ 等于 \((\qquad)\)
【难度】
【出处】
2010年复旦大学优秀高中生文化水平选拔测试
【标注】
【答案】
C
【解析】
双曲线中心为 $P\left( {1,1} \right)$．
如图．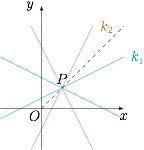
因为 ${C_1}$ 为实轴在 $y$ 轴方向上的双曲线，所以 $k_1^2 = \dfrac{{{a^2}}}{{{b^2}}}$，所以$$e_1^2 = \dfrac{{{c^2}}}{{{a^2}}} = 1 + \dfrac{{{b^2}}}{{{a^2}}} = 1 + \dfrac{1}{{k_1^2}},$$因为 ${C_2}$ 为实轴在 $x$ 轴方向上的双曲线，所以 $k_2^2 = \dfrac{{{b^2}}}{{{a^2}}}$，所以$$e_2^2 = 1 + \dfrac{{{b^2}}}{{{a^2}}} = 1 + k_2^2.$$因此$$\dfrac{{{e_1}}}{{{e_2}}} = \sqrt {\dfrac{{1 + \dfrac{1}{{k_1^2}}}}{{1 + k_2^2}}} = \sqrt {\dfrac{{k_1^2 + 1}}{{k_1^2 + k_1^2k_2^2}}} = 1.$$
如图．
因为 ${C_1}$ 为实轴在 $y$ 轴方向上的双曲线，所以 $k_1^2 = \dfrac{{{a^2}}}{{{b^2}}}$，所以$$e_1^2 = \dfrac{{{c^2}}}{{{a^2}}} = 1 + \dfrac{{{b^2}}}{{{a^2}}} = 1 + \dfrac{1}{{k_1^2}},$$因为 ${C_2}$ 为实轴在 $x$ 轴方向上的双曲线，所以 $k_2^2 = \dfrac{{{b^2}}}{{{a^2}}}$，所以$$e_2^2 = 1 + \dfrac{{{b^2}}}{{{a^2}}} = 1 + k_2^2.$$因此$$\dfrac{{{e_1}}}{{{e_2}}} = \sqrt {\dfrac{{1 + \dfrac{1}{{k_1^2}}}}{{1 + k_2^2}}} = \sqrt {\dfrac{{k_1^2 + 1}}{{k_1^2 + k_1^2k_2^2}}} = 1.$$
题目
答案
解析
备注
